高考押题最后一卷_高考最后压轴题

1.2011年广东高考物理最后一道压轴题的第2小题不懂，盼讲解，谢谢!

2.2022年高考数学压轴题解题思路

3.06上海高考数学最后一题详解

4.天津物理高考最后一道大题多少分

5.高考数学压轴题是第几题

6.1996年高考数学的最后一道压轴题的题目及答案（需要详细过程）

一般高考最后的一道压轴题的考试难度是最大的，因为其综合性比较强，即使是数学比比较不错的的考生，最后的一道题也很少能得满分。

并且最后一道压轴题的分数一般还比较高，想要高考数学能够得高分，那么最后一道大题必须不能丢太多的分数，一般最后一道压轴题的考试出题点基本上固定的，一般都是解析几何、数列、导数等，或者综合性大一些的还可能涉及多一些的知识点。

如果应对高考数学最后一道压轴题

高考数学的出题点基本上我们都有所了解，所以在平时备考的时候应该注意有针对性的练习，适当地去做专项练习，在平时备考的时候做一些考试的大题，然后加强对知识点的理解，熟悉考试题型和考试内容，对于有问题不理解的地方找老师或者数学比比较不错的的同学帮助讲解，帮助自己了解相应的思路逻辑，下次出现类似的题型能够更加轻松的应对。

2011年广东高考物理最后一道压轴题的第2小题不懂，盼讲解，谢谢!

高考数学的最后一道大题，对于很多高三学生来说就是一个噩梦，因为它涉及的知识面比较广，对学生扩展性思维能力要求非常高。而且还需要你将前后知识充分的人会贯通，思维跳跃能力要比较好，对整个题目要纵观全局，一步紧接这一步，环环相扣，还不一定能将它解出来。

我在高考前复习的那段时间，还没有完全放弃最后一道大题，有时候做完一套数学模拟题，我也会试着去钻研一下最后一个大题。在往往是想破脑袋也只能做出来前两问，后面两问看答案就有三四页，能把那些步骤看懂就已经很不错了。

有一次我拿着最后一道大题去问老师，老师拿着那道题研究了一个多小时才做出来，给我讲了半天我也没听懂。老师就会很无奈的说，你自己拿着看一下吧！能看懂多少是多少，这个题对你们来说有点难。

后来复习的那段时间，我几乎都放弃最后一道大题了！即使做也就是象征性的做一下第一问，其他的就不管了。因为做起来太浪费时间了，还不一定能够得分，高考最重要的还是要拿到分数。

最后一道大题考的综合知识能力比较强。如果想把它全部答对，是非常不容易的。高考时间非常紧迫，我们根本没有时间去做。但是我们可以冲着题目的意思，先把自己知道的值算出来。阅卷老师会给我们酌情给分，也不至于全军覆没。

2022年高考数学压轴题解题思路

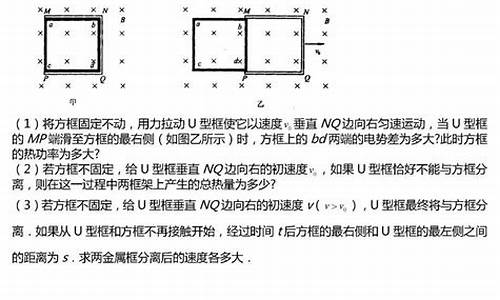
恩。。这道题首先用动量定理加动能定理算出各自需要多少路程达到共同速度。这样做的原因是因为涉及路程判断，所以不牵涉时间比较好做。算出木块要滑2R才达到共同速度，并且相对位移为6R（第三个方程应该是μmgx2=1/2Mv^2，答案错了）然后判断就好多了

1： 当R<L<2R时 首先应该知道当滑完全程的动能损耗 μmg（6.5R+2R）<9/2mgR 所以一定会划过去。所以WF=μmg（L+6.5R）

2：当2R<L<5R时分析运动状况是先达到公共速度。然后没有磨损。碰撞后滑完剩下的0.5R。 μmg（6.5R+2R）<9/2mgR所以WF=μmg（8R+0.5R）是不变的。最后用一个简单的动能判断就行了，

06上海高考数学最后一题详解

很多高中生都会面临高考 数学 130分上不去的瓶颈，这其中很大一部分的原因都出在压轴题上。下面我整理了一些高考数学压轴题的解题思路，供大家参考！

1、复杂的问题简单化，就是把一个复杂的问题，分解为一系列简单的问题，把复杂的图形，分成几个基本图形，找相似，找直角，找特殊图形，慢慢求解，高考是分步得分的，这种思考方式尤为重要，能算的先算，能证的先证，踏上要点就能得分，就算结论出不来，中间还是有不少分能拿。

2、一般的问题特殊化，有些一般的结论，找不到一般解法，先看特殊情况，比如动点问题，看看运动到中点怎样，运动到垂直又怎样，变成等腰三角形又会怎样，先找出结论，再慢慢求解。

3、运动的问题静止化，对于动态的图形，先把不变的线段，不变的角找到，有没有始终相等的线段，始终全等的图形，始终相似的图形，所有的运算都基于它们，在找到变化线段之间的联系，用代数式慢慢求解。

最牛高考励志书，淘宝搜索《高考蝶变》购买！

1.圆锥曲线

圆锥曲线题，第一问求曲线方程，注意方法(定义法、待定系数法、直接求轨迹法、反求法、参数方程法等等)。一定检查下第一问算的数对不，要不如果算错了第二问做出来了也白算了。

第二问有直线与圆锥曲线相交时，记住“联立完事用联立”，第一步联立，根据韦达定理得出两根之和、两根之差、因一般都是交于两点，注意验证判别式>;0，设直线时注意讨论斜率是否存在。

第二步也是最关键的就是用联立，关键是怎么用联立，即如何将题里的条件转化成你刚才联立完的x1+x2和x1x2，然后将结果代入即可，通常涉及的题型有弦长问题(代入弦长公式)、定比分点问题(根据比例关系建立三点坐标之间的一个关系式(横坐标或纵坐标)，再根据根与系数的关系建立圆锥曲线上的两点坐标的两个关系式，从这三个关系式入手解决)、点对称问题(利用两点关于直线对称的两个条件，即这两点的连线与对称轴垂直和这两点的中点在对称轴上)、定点问题(直线y=kx+b过定点即找出k与b的关系。

2.立体几何

立体几何题，证明题注意各种证明类型的方法(判定定理、性质定理)，注意引辅助线，一般都是对角线、中点、成比例的点、等腰等边三角形中点等等，理科其实证明不出来直接用向量法也是可以的。计算题主要是体积，注意将字母换位(等体积法);

线面距离用等体积法。理科还有求二面角、线面角等，用建立空间坐标系的方法(向量法)比较简单，注意各个点的坐标的计算，不要算错。

我推荐： 高考数学最难的压轴题破解

3.导数

高考导数压轴题考察的是一种综合能力，其考察内容方法远远高于课本，其涉及基本概念主要是：切线，单调性，非单调，极值，极值点，最值，恒成立，任意，存在等。

1.一般题目中会有少量文字描述，所以就会涉及文字的简单翻译。

2.题目中最核心的描述为各类式子：主要为普通类型：一般涉及三次函数，指对数，分式函数，绝

天津物理高考最后一道大题多少分

题目可以给我看一下么

否则怎么做?

首先说一句 这是你的不准时

我昨天等了一晚上

这题还好,但作为压轴题,难度就不大了

具体过程我大概写一下

不懂得你可以来问我

首先说一下思路

因为做这种题的惯性思维之一是

看到题目条件N是正整数,联系上两题想到讨论奇偶

然后个人觉得因为2)问已经有个小证明可以借鉴

证法如下:

当N为偶数时设y2=x2^n+a/x2^n y1=x1^n+a/x1^2

那么化简得y2-y1=(x2^n-x1^n)(1-a/x1^n*x2^n)

显然当a的根号2n次方<x1<x2时,

有y2>y1, 函数递增 即x大于a的根号2n次方时递增

同理在(0,a的根号2n次方)递减,

又因为N为偶数,所以是偶函数...

所以根据对称性可得两个区间

同理当N为奇数市 原函数为奇函数

那么同理易知单调区间

其实很简单 就是比较难打

然后你应该会了

就是用均值不等式做

所以1时最小

1/2 2时最大

得到两解....

不懂的可以问我

但不要把自己的原因推到别人身上

如果是我求别人

我不会耍大牌

让别人主动找我的

因为帮你的人有他自己要做的事

并不是那么闲

:)

祝高考成功

高考数学压轴题是第几题

18分。高考物理是我们人生当中最重要的一门科目，而且它的难度也是非常高的，在天津物理高考的最后一题的通常都是压轴题，它的分值是非常大的，通常来讲有2到3个小题，第一、二个小题的得分通常都是四分左右，第三小题的分数一般都是十分。

1996年高考数学的最后一道压轴题的题目及答案（需要详细过程）

高考数学压轴题指的是选择题的最后一题，填空题的最后一题，以及大题的最后两题。一般选择和填空考察的内容比较广泛，考察形式比较灵活，每个章节都可能出在最后一题，但是考察函数和解析几何的概率比较大。最后两个大题，一般都是函数和解析几何，函数题一般会和其他的模块进行结合，比如说平面向量，三角函数，数列等等，综合性比较强，解析几何一般会涉及动点问题。

(Ⅰ)证明：由条件当－1≤x≤1时，│f(x)│≤1，取x=0得│c│=│f(0)│≤1，即│c│≤1． (Ⅱ)：当a>0时，g(x)=ax+b在[－1，1]上是增函数，∴g(－1)≤g(x)≤g(1)，∵│f(x)│≤1 (－1≤x≤1)，│c│≤1，∴g(1)=a+b=f(1)－c≤│f(1)│+│c│≤2，g(－1)=－a+b=－f(－1)+c≥－(│f(－1)│+│c│)≥－2， 由此得│g(x)│≤2; 当a<0时，g(x)=ax+b在[－1，1]上是减函数，∴g(－1)≥g(x)≥g(1)，∵│f(x)│≤1 (－1≤x≤1)，│c│≤1，∴g(－1)=－a+b=－f(－1)+c≤│f(－1)│+│c│≤2，g(1)=a+b=f(1)－c≥－(│f(1)│+│c│)≥－2，由此得│g(x)│≤2; 当a=0时，g(x)=b，f(x)=bx+c．∵－1≤x≤1，∴│g(x)│=│f(1)－c│≤│f(1)│+│c│≤2．综上得│g(x)│≤2．(Ⅲ)因为a>0，g(x)在[－1，1]上是增函数，当x=1时取得最大值2，即g(1)=a+b=f(1)－f(0)=2． ①∵－1≤f(0)=f(1)－2≤1－2=－1，∴c=f(0)=－1． 因为当－1≤x≤1时，f(x)≥－1，即f(x)≥f(0)，根据二次函数的性质，直线x=0为f(x)的图像的对称轴，由此得 由① 得a=2．所以 f(x)=2x2－1．