高考函数经典例题,高考函数题理科

1.高三数学函数综合题

2.高考 三角函数题

3.一道高中数学函数题 快高考了谢谢大家~

4.问一题关于函数的数学题``后天就要高考嘞``

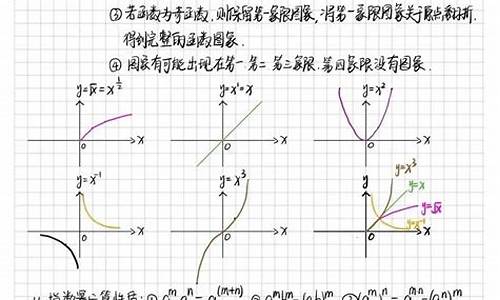
1,若x是方程lgx+x=2的解，求x属于的区间。 2，把函数y=lg(2x)的图像a平移，得到函数y=lg(x-1)的图像，求a. 3,设函数f(x)=cos(x的绝对值+30度）（x是实数),求函数单调区间。 4，若函数f(x)=(X^2+bx+c)e^-x在（负无穷，-1），（1，正无穷）上单调递减，在（-1,1）单调递增，求b+c的值。 5，画出函数y=(2^x+1)\（2^x-1)的大致图像。 6，依次画出3^x,3^x+1,3^(x+1),3^x的绝对值的图像， 7，sin(x）经怎样变换得Asin(wx+b)+c,请用两种方法说明。 8，(ax+b)\(cx+d)的图像的中心对称点及变换方式。 9，f(x)图像关于原点坐标对称的图像恰好为y=3-2x的图像，求f（x). 10,e^x按照向量a=(2,3)平移得到新函数g(x），求g(x). 只是些容易题 ，做好这些，你就可以去做高考题啦！（结果如何，概不负责）但还是给点分额吧！

高三数学函数综合题

讲解（纯手打，解题步骤，可参照之前那位网友的）：

（1）这一问是一个恒成立问题，对于恒成立问题，一般是要求出最值的，题中说：

f（x）≥0恒成立，这就说明在函数定义域内，f（x）的最小值要大于或等于0，相对的如果题目说f（x）≤0，则说明函数最大值要小于或等于0，那么问题就转化成求函数最值的问题，由于高中所学的函数全是初等函数，所以在定义域内一定可导，所以只要在定义域内你大可放心去求导，进而去求极值，本题只有极小值，所以也是最小值（如果有极大值又有极小值，或者含有边界值，则要根据题意，比较出一个最大值或是最小值），求出的极小值是，当x=lna时，f(x)为极小值，即f(lna)≥0，解出a≤1，则a最大值为1

（2）这一问仍然是恒成立问题，所以仍然需要求最值，由斜率问题联想到导数，写出AB斜率的表达式，并且代入g(x)表达式，式子，就是答案里的式子（答案中的式子，其实是拉格朗日中值定理的变形，因为高中不学这个定理），把式子变形得到，g(x2)-mx2 ＞ g(x1)-mx1， 到这问题的核心就出现了! 由AB斜率大于m恒成立，将这个条件转化为g(x2)-mx2 ＞ g(x1)-mx1恒成立，这两个式子在题目所给的条件下是等价的，所以你解出g(x2)-mx2 ＞ g(x1)-mx1，也就解出了原题。

现在就是对g(x2)-mx2 ＞ g(x1)-mx1这类式子的处理了，这类式子的共同特点就不等号左右两边的表达式的形式是一样的，那么遇到这种证明恒成立的问题，你可以向这个方面考虑，具体方法就是：令一个函数F（x）=不等号一边的式子，将X1或X2改成x，本题就是F（x）=g(x)-mx，而一般遇到X1≠X2，则可以直接令X1＞X2，或X1＜X2，这样就转化成F(X1)与F(X2)，比较大小的问题了，那么对于函数在不同点的大小问题可以用函数的单调性来解答，进而去判断F(X)的单调性，很自然地就是求导，在这时，你如果是令X2＞X1，那么F(X)就是单调增函数（对于本题而言），那么解答就如答案所示，如果你令X2<X1，那么F(X)就是单调递减，则解出m≥g'(x)，因为g'(x)≥3，那么是无法定出m的准确取值范围，所以舍去。

综上只有F(X)单调递增时，m的范围可以确定，那么顺着这个思路往下解，用一次基本不等式，然后定出m的范围即可。

（3）遇到这种题目，你先看给出的问题能否变形，因为题目如果想出的难一点，是不会直接提出问题的核心的，需要自己去观察，然后找到核心问题，本题，不等式右边明显有个（2n）^n，这和左边的形式相同，所以先变形，把式子化成（1/2n）^n+(3/2n)^n+……+((2n-1)/2n)^n<√e/(e-1)，而此时全看你能不能想到用第一问的条件，用的话，这相当于让你有依据去放缩，否则直接放缩很难证到题目所要的结果，此时就可以按照答案所示的方法，令X=（如答案所示），其实，你可以把a带着，就是e^x≥a(x+1)，求到最后，你会发现，如果要满足题意，a就是1，答案那样写的话，就相当于直接告诉你a=1。这种题一般是连在题目的最后一问，如果遇到，就往上找，看能不能用已经证出的条件来解答，能想到，基本就能做出来。这问最后不等号右边是等比数列求和，自己算一下就行了。

给你提条建议，把这类题目整理出来，从中归纳解题的技巧，如找相同的特点，相同的形式，或是类似的问法，然后自己总结成适合自己的理解方式，再加以做题巩固就行了。

纯手打，记得采纳哦~

高考 三角函数题

（1）-1<a<0或a>1

g(x)在区间[1,2]单调，则a+1>0，且a+1不等于1，所以a>-1，且a不等于0

且-1<a<0时，g(x)单调减；且a>0时，g(x)单调增

当-1<a<0时，区间[1,2]上，1/2x^2和alnx都单调减，则f(x)单调减，满足同单调性

当a>0时，在区间[1,2]上，1/2x^2单调减，alnx单调增，则f(x)无法直接判断单调性,对f(x)求导，f'(x) = -1/x^3 + a/x，只有f'(x)>0,才能保证f(x)单调增

把a/x和1/x^3的函数曲线画在一起就能看出来，只有当a>1时， a/x-1/x^3在[1,2]上才恒大于0，此时f(x)单调增

综上，-1<a<0或a>1

一道高中数学函数题 快高考了谢谢大家~

第3题这种类型的题的解法是：

把sinxcosx化成sinx+cosx的形式，然后设sinx+cosx=t，再根据t的范围求解函数的最值，如下：

设t=sinx+cosx

那么t=sinx+cosx

=√2[(√2/2)sinx+(√2/2)cosx]

=√2[cos(π/4)sinx+sin(π/4)cosx]

=√2sin(x+π/4)

∴t∈[-√2，√2]

又∵t?=(sinx+cosx)?

=sin?x+2sinxcosx+cos?x

=1+2sinxcosx

∴sinxcosx=(t?-1)/2

∴y=[(t?-1)/2]+t，t∈[-√2，√2]

抛物线y的对称轴是t=-1

∴t=-1时y(min)=-1；t=√2时y(max)=(√2)+1/2

或者化成完全平方加一个常数的形式：y=(1/2)(t+1)?-1来计算也很容易。

括号打的有点多，怕你误解，相信以你的水平也不会，肯定能看懂的是吧！

总之，对于三角函数的计算要把公式与公式的转化运用的非常熟练，另外做过的题一定要看到题就想到思路，不要过一段时间再回来做就忘的差不多了那样的，到高考会很纠结的。

还有一种解法是求导，不知你们现在高中学了没，反正我们那时候好像没学过积的导数，三角函数的导数公式忘了学过没。。。(sinx)＇=cosx；(cosx)＇=-sinx

方法如下：(积的导数公式：(uv)＇=u＇×v+u×v＇，其中u，v都是x的函数)

y＇=(sinx)＇cosx+sinx(cosx)＇+(sinx)＇+(cosx)＇

=cos?x-sin?x+cosx-sinx

=(cosx-sinx)(cosx+sinx+1)

=√2cos(x+π/4)[√2sin(x+π/4)+1]

令y＇=0，得cos(x+π/4)=0或√2sin(x+π/4)+1=0

得x+π/4=(2m+1)π或x=(2k-1/2)π±π/4

再代入求最值，当然这个比较麻烦点，在某些场合用导数会更简便。

对于三角函数，不到万不得已不要用万能公式，另外你们应该也做过用万能公式的题，也就那些题型记住就行了，其他的看着办。

第5题，看来你基础知识没学好，把高一第一册课本的奇偶函数那一节翻出来看是怎么定义的！

奇函数可以这么理解：定义域关于原点对称，函数图象关于原点对称，对于三角函数来说，在定义域关于原点对称的基础上，只要函数过原点，也就是把点(0，0)代入可以使方程成立那么就是奇函数。

相应地，偶函数是定义域关于原点对称，函数图象关于y轴对称的函数。对于三角函数来说，定义域关于原点对称的基础上，x=0是函数的一个极值点就是偶函数，也就是在图象上x=0的点是最高点或者最低点，或者在x=0处的导数等于0，都是可以用来判定的。

你这个例子，你们老师说把它当整体看，是说括号内整体等于t，那么t=0时cosx取最大值，但是此时x=-9π/4≠0，也就是说x和t不是同一个概念，x=-9π/4才是f(x)的对称轴。反过来看，当x=0时t=9π/2，f(0)=0，也就是过原点，是奇函数。

你所认为的cosx是偶函数，是标准的余弦函数，也就是不平移，不伸缩，但是f(x)是在cosx的基础上平移和伸缩了的，当你把cosx向右平移π/2时就变成了sinx的标准情况，也就是y=cos(x-π/2)是奇函数，所以不能笼统的说以cos开头的函数就是偶函数，还是得求对称轴的。

其他的题应该是比较简单的，我有时间再算，挺忙的。有不懂的再留言！

希望能给你带来帮助。

问一题关于函数的数学题``后天就要高考嘞``

令x=tant，则y（t）=m*sint*2+4*3^1/2*sint+n*cos^2，用二倍角公式化简，y（t）=2*3^1/2sin2t+(n-m)/2*cos2t+(n+m)/2=(12+((n-m)/2)^2)^1/2*sin(2t+a)+(n+m)/2，y(t)max=(12+((n-m)/2)^2)^1/2+(n+m)/2=7，y(t)min=—(12+((n-m)/2)^2)*1/2+(n+m)/2=—1，m=1，n=5或m=5，n=1。

由于f是偶函数，所以在y轴两侧对称；

由于f(1/3)=0且f在正轴上递增，所以f在（-1/3，1/3）上小于0；

由上面的分析，我们要求x满足：

1，使log1/8 X有意义，即x〉0；

2，使log1/8 X大于1/3或者小于-1/3.

再注意到log1/8 X关于x单调减少，于是x的取值范围是

0<x<(1/8)^(1/3)=1/2,或者

x>(1/8)^(-1/3)=2

整理可得：（0，1/2）并上（2,正无穷）