三角函数高考专题_三角函数高考专题讲座

1.必修3三角函数 一道高考题

2.一道有关三角函数的数学高考题

3.求解高考三角函数题

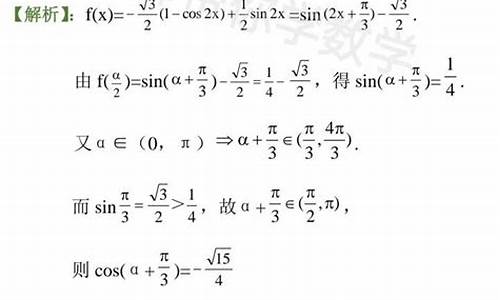
第3题这种类型的题的解法是：

把sinxcosx化成sinx+cosx的形式，然后设sinx+cosx=t，再根据t的范围求解函数的最值，如下：

设t=sinx+cosx

那么t=sinx+cosx

=√2[(√2/2)sinx+(√2/2)cosx]

=√2[cos(π/4)sinx+sin(π/4)cosx]

=√2sin(x+π/4)

∴t∈[-√2，√2]

又∵t?=(sinx+cosx)?

=sin?x+2sinxcosx+cos?x

=1+2sinxcosx

∴sinxcosx=(t?-1)/2

∴y=[(t?-1)/2]+t，t∈[-√2，√2]

抛物线y的对称轴是t=-1

∴t=-1时y(min)=-1；t=√2时y(max)=(√2)+1/2

或者化成完全平方加一个常数的形式：y=(1/2)(t+1)?-1来计算也很容易。

括号打的有点多，怕你误解，相信以你的水平也不会，肯定能看懂的是吧！

总之，对于三角函数的计算要把公式与公式的转化运用的非常熟练，另外做过的题一定要看到题就想到思路，不要过一段时间再回来做就忘的差不多了那样的，到高考会很纠结的。

还有一种解法是求导，不知你们现在高中学了没，反正我们那时候好像没学过积的导数，三角函数的导数公式忘了学过没。。。(sinx)＇=cosx；(cosx)＇=-sinx

方法如下：(积的导数公式：(uv)＇=u＇×v+u×v＇，其中u，v都是x的函数)

y＇=(sinx)＇cosx+sinx(cosx)＇+(sinx)＇+(cosx)＇

=cos?x-sin?x+cosx-sinx

=(cosx-sinx)(cosx+sinx+1)

=√2cos(x+π/4)[√2sin(x+π/4)+1]

令y＇=0，得cos(x+π/4)=0或√2sin(x+π/4)+1=0

得x+π/4=(2m+1)π或x=(2k-1/2)π±π/4

再代入求最值，当然这个比较麻烦点，在某些场合用导数会更简便。

对于三角函数，不到万不得已不要用万能公式，另外你们应该也做过用万能公式的题，也就那些题型记住就行了，其他的看着办。

第5题，看来你基础知识没学好，把高一第一册课本的奇偶函数那一节翻出来看是怎么定义的！

奇函数可以这么理解：定义域关于原点对称，函数图象关于原点对称，对于三角函数来说，在定义域关于原点对称的基础上，只要函数过原点，也就是把点(0，0)代入可以使方程成立那么就是奇函数。

相应地，偶函数是定义域关于原点对称，函数图象关于y轴对称的函数。对于三角函数来说，定义域关于原点对称的基础上，x=0是函数的一个极值点就是偶函数，也就是在图象上x=0的点是最高点或者最低点，或者在x=0处的导数等于0，都是可以用来判定的。

你这个例子，你们老师说把它当整体看，是说括号内整体等于t，那么t=0时cosx取最大值，但是此时x=-9π/4≠0，也就是说x和t不是同一个概念，x=-9π/4才是f(x)的对称轴。反过来看，当x=0时t=9π/2，f(0)=0，也就是过原点，是奇函数。

你所认为的cosx是偶函数，是标准的余弦函数，也就是不平移，不伸缩，但是f(x)是在cosx的基础上平移和伸缩了的，当你把cosx向右平移π/2时就变成了sinx的标准情况，也就是y=cos(x-π/2)是奇函数，所以不能笼统的说以cos开头的函数就是偶函数，还是得求对称轴的。

其他的题应该是比较简单的，我有时间再算，挺忙的。有不懂的再留言！

希望能给你带来帮助。

必修3三角函数 一道高考题

数学知识点很多，只有进行 总结 ，才能发现重点难点，下面就是我给大家带来的，希望大家喜欢！

高考数学公式总结

高考数学三角函数公式

sinα=∠α的对边/斜边

cosα=∠α的邻边/斜边

tanα=∠α的对边/∠α的邻边

cotα=∠α的邻边/∠α的对边

倍角公式

Sin2A=2SinA?CosA

Cos2A=CosA2-SinA2=1-2SinA2=2CosA2-1

tan2A=(2tanA)/(1-tanA2)

(注：SinA2是sinA的平方sin2(A))

三倍角公式

sin3α=4sinα·sin(π/3+α)sin(π/3-α)

cos3α=4cosα·cos(π/3+α)cos(π/3-α)

tan3a=tana·tan(π/3+a)·tan(π/3-a)

三倍角公式推导

sin3a=sin(2a+a)=sin2acosa+cos2asina

三角函数角公式

Asinα+Bcosα=(A2+B2)’(1/2)sin(α+t)，其中

sint=B/(A2+B2)’(1/2)

cost=A/(A2+B2)’(1/2)

tant=B/A

Asinα+Bcosα=(A2+B2)’(1/2)cos(α-t)，tant=A/B

降幂公式

sin2(α)=(1-cos(2α))/2=versin(2α)/2

cos2(α)=(1+cos(2α))/2=covers(2α)/2

tan2(α)=(1-cos(2α))/(1+cos(2α))

三角函数推导公式

tanα+cotα=2/sin2α

tanα-cotα=-2cot2α

1+cos2α=2cos2α

1-cos2α=2sin2α

1+sinα=(sinα/2+cosα/2)2=2sina(1-sin2a)+(1-2sin2a)sina=3sina-4sin3a

cos3a=cos(2a+a)=cos2acosa-sin2asina=(2cos2a-1)cosa-2(1-sin2a)cosa=4cos3a-3cosa

sin3a=3sina-4sin3a=4sina(3/4-sin2a)=4sina[(√3/2)2-sin2a]=4sina(sin260°-sin2a)=4sina(sin60°+sina)(sin60°-sina)=4sina 2sin[(60+a)/2]cos[(60°-a)/2] 2sin[(60°-a)/2]cos[(60°-a)/2]=4sinasin(60°+a)sin(60°-a)

cos3a=4cos3a-3cosa=4cosa(cos2a-3/4)=4cosa[cos2a-(√3/2)2]=4cosa(cos2a-cos230°)=4cosa(cosa+cos30°)(cosa-cos30°)=4cosa 2cos[(a+30°)/2]cos[(a-30°)/2] {-2sin[(a+30°)/2]sin[(a-30°)/2]}=-4cosasin(a+30°)sin(a-30°)=-4cosasin[90°-(60°-a)]sin[-90°+(60°+a)]=-4cosacos(60°-a)[-cos(60°+a)]=4cosacos(60°-a)cos(60°+a)

上述两式相比可得

tan3a=tanatan(60°-a)tan(60°+a)

三角函数半角公式

tan(A/2)=(1-cosA)/sinA=sinA/(1+cosA);

cot(A/2)=sinA/(1-cosA)=(1+cosA)/sinA.

sin2(a/2)=(1-cos(a))/2

cos2(a/2)=(1+cos(a))/2

tan(a/2)=(1-cos(a))/sin(a)=sin(a)/(1+cos(a))

三角函数三角和

sin(α+β+γ)=sinα·cosβ·cosγ+cosα·sinβ·cosγ+cosα·cosβ·sinγ-sinα·sinβ·sinγ

cos(α+β+γ)=cosα·cosβ·cosγ-cosα·sinβ·sinγ-sinα·cosβ·sinγ-sinα·sinβ·cosγ

tan(α+β+γ)=(tanα+tanβ+tanγ-tanα·tanβ·tanγ)/(1-tanα·tanβ-tanβ·tanγ-tanγ·tanα)

三角函数两角和差

cos(α+β)=cosα·cosβ-sinα·sinβ

cos(α-β)=cosα·cosβ+sinα·sinβ

sin(α±β)=sinα·cosβ±cosα·sinβ

tan(α+β)=(tanα+tanβ)/(1-tanα·tanβ)

tan(α-β)=(tanα-tanβ)/(1+tanα·tanβ)

三角函数和差化积

sinθ+sinφ=2sin[(θ+φ)/2]cos[(θ-φ)/2]

sinθ-sinφ=2cos[(θ+φ)/2]sin[(θ-φ)/2]

cosθ+cosφ=2cos[(θ+φ)/2]cos[(θ-φ)/2]

cosθ-cosφ=-2sin[(θ+φ)/2]sin[(θ-φ)/2]

tanA+tanB=sin(A+B)/cosAcosB=tan(A+B)(1-tanAtanB)

tanA-tanB=sin(A-B)/cosAcosB=tan(A-B)(1+tanAtanB)

三角函数积化和差

sinαsinβ=[cos(α-β)-cos(α+β)]/2

cosαcosβ=[cos(α+β)+cos(α-β)]/2

sinαcosβ=[sin(α+β)+sin(α-β)]/2

cosαsinβ=[sin(α+β)-sin(α-β)]/2

三角函数诱导公式

sin(-α)=-sinα

cos(-α)=cosα

tan(—a)=-tanα

sin(π/2-α)=cosα

cos(π/2-α)=sinα

sin(π/2+α)=cosα

cos(π/2+α)=-sinα

sin(π-α)=sinα

cos(π-α)=-cosα

sin(π+α)=-sinα

cos(π+α)=-cosα

tanA=sinA/cosA

tan(π/2+α)=-cotα

tan(π/2-α)=cotα

tan(π-α)=-tanα

tan(π+α)=tanα

诱导公式记背诀窍：奇变偶不变，符号看象限

万能公式

sinα=2tan(α/2)/[1+tan’(α/2)]

cosα=[1-tan’(α/2)]/1+tan’(α/2)]

tanα=2tan(α/2)/[1-tan’(α/2)]

其它 公式

(1)(sinα)2+(cosα)2=1

(2)1+(tanα)2=(secα)2

(3)1+(cotα)2=(cscα)2

证明下面两式,只需将一式,左右同除(sinα)2,第二个除(cosα)2即可

(4)对于任意非直角三角形,总有

tanA+tanB+tanC=tanAtanBtanC

证:A+B=π-Ctan(A+B)=tan(π-C)

(tanA+tanB)/(1-tanAtanB)=(tanπ-tanC)/(1+tanπtanC)

整理可得tanA+tanB+tanC=tanAtanBtanC

得证同样可以得证,当x+y+z=nπ(n∈Z)时,该关系式也成立

由tanA+tanB+tanC=tanAtanBtanC可得出以下结论

(5)cotAcotB+cotAcotC+cotBcotC=1

(6)cot(A/2)+cot(B/2)+cot(C/2)=cot(A/2)cot(B/2)cot(C/2)

(7)(cosA)2+(cosB)2+(cosC)2=1-2cosAcosBcosC

(8)(sinA)2+(sinB)2+(sinC)2=2+2cosAcosBcosC

(9)sinα+sin(α+2π/n)+sin(α+2π 2/n)+sin(α+2π 3/n)+……+sin[α+2π (n-1)/n]=0

cosα+cos(α+2π/n)+cos(α+2π 2/n)+cos(α+2π 3/n)+……+cos[α+2π (n-1)/n]=0以及

sin2(α)+sin2(α-2π/3)+sin2(α+2π/3)=3/2

tanAtanBtan(A+B)+tanA+tanB-tan(A+B)=0

高考数学 记忆 方法

一、分类记忆法

遇到数学公式较多，一时难于记忆时，可以将这些公式适当分组。例如求导公式有18个，就可以分成四组来记：(1)常数与幂函数的导数(2个);(2)指数与对数函数的导数(4个);(3)三角函数的导数(6个);(4)反三角函数的导数(6个)。求导法则有7个，可分为两组来记：(1)和、差、积、商复合函数的导数(4个);(2)反函数、隐函数、幂指数函数的导数(3个)。

二、推理记忆法

许多数学知识之间逻辑关系比较明显，要记住这些知识，只需记忆一个，而其余可利用推理得到，这种记忆称为推理记忆。例如，平行四边形的性质，我们只要记住它的定义，由定义推理得它的任一对角线把它平分成两个全等三角形，继而又推得它的对边相等，对角相等，相邻角互补，两条对角线互相平分等性质。

三、标志记忆法

在学习某一章节知识时，先看一遍，对于重要部分用彩笔在下面画上波浪线，再记忆时，就不需要将整个章节的内容从头到尾逐字逐句的看了，只要看划重点的地方并在它的启示下就能记住本章节主要内容，这种记忆称为标志记忆。

四、回想记忆法

在重复记忆某一章节的知识时，不看具体内容，而是通过大脑回想达到重复记忆的目的，这种记忆称为回想记忆。在实际记忆时，回想记忆法与标志记忆法是配合使用的。

高考数学复习建议

初次学习和再次复习不同。绝大部分考生在高一高二两年的时间中进行的都是新知识新理论的学习，这是初次认识初次接触的过程，我们称之为初次学习，这个过程强调的是认知、接受和掌握。而高三将近一年的时间考生几乎接触的都是之前两年当中见过的理解了的但是很多已经遗忘的内容，我们将这个过程称之为再次复习。再次复习除了恢复考生对相应知识点的记忆之外，更重要的在于将知识点升华为考点，这个过程重视的是理解、综合与应用。两个过程截然不同，必然导致我们应对的策略也要有所变化。

学习和复习的主线不同。学习的主线我们应该都很熟悉，看一看教材的目录就非常明确了：高一高二两年当中一定是以章节为单位，一个知识点接一个知识点按部就班地介绍和学习。每个章节内部也是基本遵循“定义—定理—公式—经典例题—实际应用—练习”这样由简到繁的内容安排。而二次复习如果也用这样的模式，导致的直接结果就是，考生按知识点分块的模式分章节去解题会很顺利，一旦拿过来一份高考试卷，遇到里面的综合性题目却无从下手，这就是平时考生经常遇到的问题——没有解题思路。

最有效的复习模式——以题型为主线。结合以上讨论的两点内容，建议考生在复习过程中尤其是最后一轮复习中一定要以当地高考常考题型为主线，以题型为主线逐步建立自己在考试当中的解题思路。以题型为主线的复习方式有以下三点优势：

第一，可以将零散的知识点从题型的角度进行二次深入的梳理，把知识认知阶段进化为知识应用阶段，达到高考要求。

第二，题型为主线可以简化思维过程，头脑中不再是孤零零的点，而是形成模块化的解题套路。

第三，掌握相应知识的常考题型比起简单掌握知识点能够更快更大幅度地在考试中提高分数。很多考生溺死在浩如烟海的知识点当中，尽管花了相当多的时间和精力，但是收效甚微，甚至由此认为高中数学很难学。如果能够转变一下复习思路，相信一定可以柳暗花明。

高考数学常用三角函数公式总结相关 文章 ：

★ 高考数学三角函数公式口诀

★ 高考数学常用的诱导公式总结

★ 高中数学必修四三角函数万能公式归纳

★ 三角函数的公式归纳总结

★ 必修四数学三角函数公式汇总

★ 高中数学三角函数高考题汇编

★ 高考数学常考知识点总结

★ 2020高考数学知识点总结大全

★ 高一数学必背公式及知识汇总

★ 高考数学复合函数知识点归纳

一道有关三角函数的数学高考题

（1）f（X）=cos(2x+pai/3)+sin^2x

=cos2xcos60-sin2xsinpai/3

=1/2cos2x-根号3/2sin2x+1/2-cos2x/2

=-根号3/2sin2x+1/2

所以当sin2x=-1时，f（x）取最大值：根号3/2+1/2

T=2pai/W=2pai/2=pai

（2）f(c/2)=-根号3/2sinc+1/2=-1/4

推出：sinc=根号3/2 C=60度

因为：cosB=-1/4 所以：sinB=根号15/4

sinA=(180-C-B)=sin(120-B)

=sin120cosB-cos120sinB

=-根号3/8+根号15/8

补充：(sinx)的平方=(1-cos2x)/2

求解高考三角函数题

f(x)=sinωxcosψ+cosωxsinψ+cosωxcosψ-sinωxsinψ

f(-x)=sinψcosωx-cosψsinωx-cosψcosωx+sinψsinωx

则：sinωxcosψ+cosωxsinψ+cosωxcosψ-sinωxsinψ=sinψcosωx-cosψsinωx-cosψcosωx-sinψsinωx

经过化简：2sinωxcosψ+2cosωxcosψ=2sin(ωx+ψ)

化简成这样，你能明白了么？

好久不学数学了，不知道化简得对不对，你看看然后自己想想吧~~~~

sinA+sinB=sinC………………（1）

cosA+cosB=cosC………………（2）

由（2）^2-(1)^2得

cos2A+cos2B+2(cosAcosB-sinAsinB)=cos2C

所以 2cos(A+B)cos(A-B)+2cos(A+B)=cos2C……………（3）

又由（1）^2+（2）^2得

2+2(cosAcosB+sinAsinB)=1

所以 cosAcosB+sinAsinB=cos(A-B)=-1/2………………（4）

所以由（3）得

2cos(A+B)*（-1/2）+2cos(A+B)=cos2C

所以cos2C=cos(A+B)=cosAcosB-sinAsinB………………（5）

则由（4）-（5）得

2sinAsinB=-1/2-cos2C

所以

sin平方A+sin平方B+sin平方C

=(sinA+sinB）^2-2sinAsinB+(sinC)^2

=2(sinC)^2-(-1/2-cos2C)

=2(sinC)^2+1/2+cos2C

=2(sinC)^2+1/2+1-2(sinC)^2

=3/2